SIGMA小组题为“LocalDrop: A Hybrid Regularization for Deep Neural Networks”论文被TPAMI成功录用。论文针对神经网络中常见的过拟合问题，提出了一种基于Local Rademacher complexity和Dropout的混合正则化机制，并首次在卷积层上利用局部拉德马赫理论建立了新的正则化方法。该方法通过基于局部拉德马赫复杂度（结合Dropout）的理论分析，分别在全连接层和卷积层上推出了假设函数集的局部拉德马赫复杂度的上界，利用该上界提出了新的正则函数。由于新的正则函数是非光滑凸函数，我们创造性地构建了两步优化求解方法，克服了现有的反向传播方法无法处理非光滑凸函数的问题，算法适用性得到增强。 ResNet-50的模型中，在CIFAR-10，CIFAR-100，ILSVRC-2012等数据集上的实验结果表明：利用我们提出的混合正则化方法比目前常用的深度网络方法在图像分类任务上的精度分别提升1%，1.5%，1.8%。并且我们的算法在DenseNet，PreActResNet，DPN-92等目前在图像分类任务中效果最好的不同的模型中均有0.3%-0.6%的提升。

主要公式：

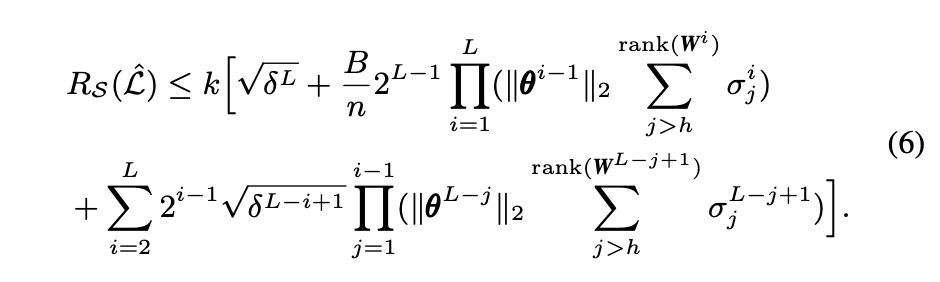公式6表示：在全连接层中，基于局部拉德马赫复杂度以及全连接网络的基本性质推导得出的假设函数集的局部拉德马赫复杂度的上界。其中k代表类别数量，δ代表局部拉德马赫复杂度中用来筛选假设函数的方差，L代表神经网络的层数，B代表输入数据的F范数的上界，n代表样本个数，θ代表每层Dropout参数的向量，W代表每层的权重矩阵，σ代表对应矩阵的奇异值，h代表的是超参。根据推导所得的上界（即公式6）简化得到全连接层网络的新的目标函数，即公式11。公式11右半部分就是提出的新正则函数。

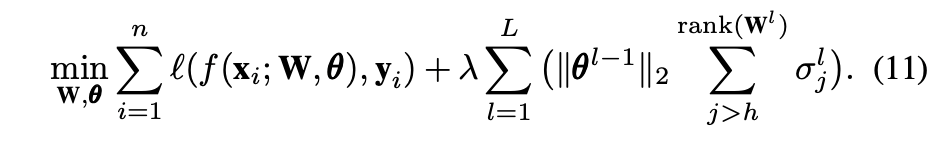上述是在全连接层的情况，然后利用杨不等式将其推广到单通道的卷积层中，再结合Dropblock推广到多通道的卷积层中，最终可得多通道卷积网络的目标函数，即公式22。其中θ、W均为分块矩阵。

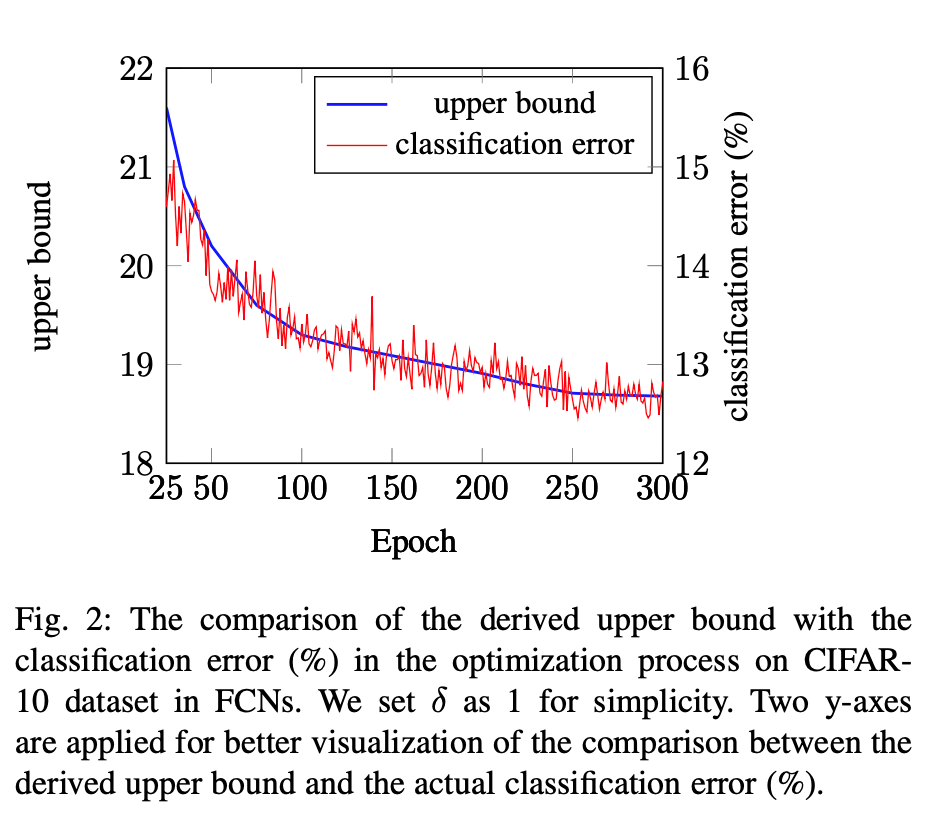
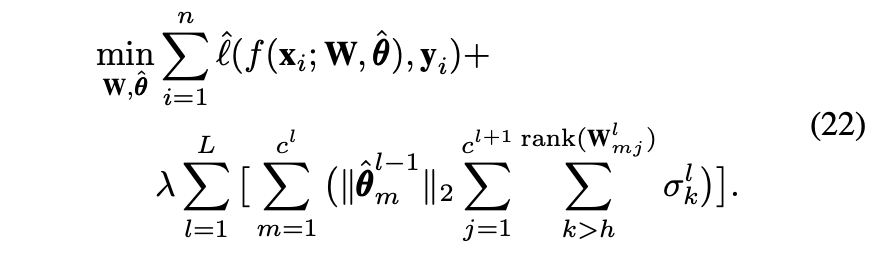利用局部拉德马赫复杂度和Dropout推出的上界和实验结果的关系如下图。蓝色的曲线代表理论推导的上界，红色的曲线代表实验中分类误差，可以看出理论和实验的结果随着网络迭代的变化是吻合的

在卷积层中结合Dropblock的网络基本结构如下图：

实验使用数据集CIFAR-10：

文章链接：https://arxiv.org/abs/2103.00719 个人简介：论文第一作者陆子青，本科毕业于复旦大学数学与应用数学专业，硕士毕业于英国杜伦大学网络系统与电子商务专业。2019年进入武汉大学计算机学院攻读博士学位。